با سلام .
مطلب جالبی رو یه جایی دیدم گفتم این جا هم بذار برای علاقمندان به ریاضی :mrgreen:
منبع :
اثبات فرمول معادلات پارامتری درون چرخ زاد
من عین مطلب رو نقل قول کردم .
عنوان : اثبات فرمول معادلات پارامتری درون چرخ زاد
سلام.
توضحاتی که میخوام بدم رو در هیچ سایت و فرومی پیدا نمیکنین. منظورم اینه که حتی تو معتبر ترین سایتهای خارجی مث ویکی پدیا هم روش اثبات فرمولهای پارامتری درون چرخزاد ها رو ننوشتن.
اول یه توضیحی برای سایر کاربران بدم که درون چرخزاد چیه؟
درون چرخزاد یا hypotrochoid (یا hypocycloid) عبارت است از اشکالی که از دوران یک دایره درون یک دایره ی دیگه به دست میاد. مانند اینها:


البته در مقابل مفهوم درون چرخزاد، مفهوم دیگری به نام برون چرخزاد هم وجود داره که تفاوتش با حالت قبل در اینه که دایره و نقطه ی متحرک همراه آن، در بیرون از دایره ی ثابت قرار دارند.
برای دیدن اشکال و توضیحات نسبی در باره ی برون چرخزادها به لینکهای زیر مراجعه کنین:
http://en.wikipedia.org/wiki/Epitrochoid
[ftp=ftp://en.wikipedia.org/wiki/Epicycloid]http://en.wikipedia.org/wiki/Epicycloid[/ftp]
---------------------
در اینگونه اشکال، 3 پارامتر مهم و تعیین کننده هستند:
1- شعاع دایره ی بزرگتر = R
2- شعاع دایره ی کوچکتر که درون دایره اول قرار گرفته است = r
3- فاصله ی نقطه ی مرجع ما که شکل را میکشد، از مرکز دایره ی کوچکتر = d
اگر در حالتی خاص d=r در نظر گرفته شود، اشکالی مانند شکل دوم بالا تشکیل میشود. در این حالت نسبت شعاع دو دایره را k نامیده و اشکال مختلف بر حسب k های متفاوت، گوناگون خواهند بود. مثالهایی از این حالت خاص را برای k های مختلف در زیر میتوانید ببینید:








اما در اینجا سعی میکنم که برای حالت کلی معادلات پارامتری رو اثبات و حل کنم.
برای راحتی مرکز دایره ی بزرگتر رو در مبدا مختصات قرار میدیم. همچنین باز برای راحتی از مختصات قطبی استفاده میکنیم. و نیز باز هم برای راحتی بیشتر در شروع حرکت، نقطه ی مرجع متحرک رو روی محور x ها در نظر میگیریم. یعنی در لحظه ی صفر داریم: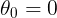
میخواهیم ببینیم در هر لحظه بر حسب ، فاصله ی متحرک مرجع ما از مبدا مختصات چقدر خواهد بود؟
، فاصله ی متحرک مرجع ما از مبدا مختصات چقدر خواهد بود؟
ذکر این نکته هم ضروریه که در حقیقت زاویه ی بین خط المرکزین دو دایره با محور x ها در هر لحظه است.
در حقیقت زاویه ی بین خط المرکزین دو دایره با محور x ها در هر لحظه است.

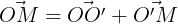
در نتیجه طول نقطه ی M (یعنی تصویر نقطه ی M روی محور x ها) برابر میشه با مجموع طول تصویرهای دو بردار 'OO و O'M.
طول تصویر بردار 'OO که به راحتی محاسبه میشود چرا که زاویه ی بین این بردار با محور x ها را میدانیم که برابر با است. پس طول تصویر بردار
است. پس طول تصویر بردار
'OO روی محور x ها برابر میشود با:

اما برای محاسبه ی طول تصویر بردار O'M لازم است که زاویه ی این بردار را با افق بدانیم. برای اینکار باید محاسبه کرد که دایره ی کوچکتر به ازای هر یک دور که روی محیط دایره ی بزرگ میزند، چند دور روی محیط خود چرخیده است؟ محیط دایره ی بزرگ برابر است با . محیط دایره ی کوچک هم برابر است با
. محیط دایره ی کوچک هم برابر است با . پس وقتی که دایره ی کوچک روی محیط دایره ی بزرگ، یک دور کامل را طی میکند، در حقیقت به اندازه ی:
. پس وقتی که دایره ی کوچک روی محیط دایره ی بزرگ، یک دور کامل را طی میکند، در حقیقت به اندازه ی:

روی محیط خودش دور زده است. پس زاویه ی بردار O'M را که آن را مینامیم این چنین بدست می آید:
را مینامیم این چنین بدست می آید:

پس حالا میتونیم مانند بردار 'OO، طول تصویر بردار O'M را بر روی محور x ها را هم حساب کنیم. این طول برابر میشود با:

بنابراین تصویر نقطه ی M روی محور x ها برابر میشه با:

با استدلالی مشابه، تصویر نقطه ی M روی محور y ها هم برابر میشه با:

اما این جوابها به خودی خود ارزش ندارند. چرا که باید در هر لحظه محاسبه کنیم که برابر با چند است و متغیر
برابر با چند است و متغیر  نیز متغیری وابسته به زمان است. اگرحرکت دایره ی کوچک را در درون دایره ی بزرگ، حرکتی یکنواخت و بدون شتاب زاویه ای فرض کنیم، فرکانس حرکت دایره ی کوچک را در درون دایره ی بزرگ مقدار ثابتی مانند f خواهد بود و
نیز متغیری وابسته به زمان است. اگرحرکت دایره ی کوچک را در درون دایره ی بزرگ، حرکتی یکنواخت و بدون شتاب زاویه ای فرض کنیم، فرکانس حرکت دایره ی کوچک را در درون دایره ی بزرگ مقدار ثابتی مانند f خواهد بود و  در هر لحظه برابر میشود با:
در هر لحظه برابر میشود با:

اما خودمان برای راحتی، قرارداد کردیم که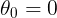 : پس داریم:
: پس داریم:

با این حساب و در نهایت مختصات نقطه ی مرجع متحرک در هر لحظه ی دلخواه t برابر است با:

******************
پنجشنبه
7 / 2 / 91
مطلب جالبی رو یه جایی دیدم گفتم این جا هم بذار برای علاقمندان به ریاضی :mrgreen:
منبع :
اثبات فرمول معادلات پارامتری درون چرخ زاد
من عین مطلب رو نقل قول کردم .
=============================================
عنوان : اثبات فرمول معادلات پارامتری درون چرخ زاد
سلام.
توضحاتی که میخوام بدم رو در هیچ سایت و فرومی پیدا نمیکنین. منظورم اینه که حتی تو معتبر ترین سایتهای خارجی مث ویکی پدیا هم روش اثبات فرمولهای پارامتری درون چرخزاد ها رو ننوشتن.
اول یه توضیحی برای سایر کاربران بدم که درون چرخزاد چیه؟
درون چرخزاد یا hypotrochoid (یا hypocycloid) عبارت است از اشکالی که از دوران یک دایره درون یک دایره ی دیگه به دست میاد. مانند اینها:


البته در مقابل مفهوم درون چرخزاد، مفهوم دیگری به نام برون چرخزاد هم وجود داره که تفاوتش با حالت قبل در اینه که دایره و نقطه ی متحرک همراه آن، در بیرون از دایره ی ثابت قرار دارند.
برای دیدن اشکال و توضیحات نسبی در باره ی برون چرخزادها به لینکهای زیر مراجعه کنین:
http://en.wikipedia.org/wiki/Epitrochoid
[ftp=ftp://en.wikipedia.org/wiki/Epicycloid]http://en.wikipedia.org/wiki/Epicycloid[/ftp]
---------------------
در اینگونه اشکال، 3 پارامتر مهم و تعیین کننده هستند:
1- شعاع دایره ی بزرگتر = R
2- شعاع دایره ی کوچکتر که درون دایره اول قرار گرفته است = r
3- فاصله ی نقطه ی مرجع ما که شکل را میکشد، از مرکز دایره ی کوچکتر = d
اگر در حالتی خاص d=r در نظر گرفته شود، اشکالی مانند شکل دوم بالا تشکیل میشود. در این حالت نسبت شعاع دو دایره را k نامیده و اشکال مختلف بر حسب k های متفاوت، گوناگون خواهند بود. مثالهایی از این حالت خاص را برای k های مختلف در زیر میتوانید ببینید:
اما در اینجا سعی میکنم که برای حالت کلی معادلات پارامتری رو اثبات و حل کنم.
برای راحتی مرکز دایره ی بزرگتر رو در مبدا مختصات قرار میدیم. همچنین باز برای راحتی از مختصات قطبی استفاده میکنیم. و نیز باز هم برای راحتی بیشتر در شروع حرکت، نقطه ی مرجع متحرک رو روی محور x ها در نظر میگیریم. یعنی در لحظه ی صفر داریم:
میخواهیم ببینیم در هر لحظه بر حسب
ذکر این نکته هم ضروریه که

در نتیجه طول نقطه ی M (یعنی تصویر نقطه ی M روی محور x ها) برابر میشه با مجموع طول تصویرهای دو بردار 'OO و O'M.
طول تصویر بردار 'OO که به راحتی محاسبه میشود چرا که زاویه ی بین این بردار با محور x ها را میدانیم که برابر با
'OO روی محور x ها برابر میشود با:
اما برای محاسبه ی طول تصویر بردار O'M لازم است که زاویه ی این بردار را با افق بدانیم. برای اینکار باید محاسبه کرد که دایره ی کوچکتر به ازای هر یک دور که روی محیط دایره ی بزرگ میزند، چند دور روی محیط خود چرخیده است؟ محیط دایره ی بزرگ برابر است با
روی محیط خودش دور زده است. پس زاویه ی بردار O'M را که آن
پس حالا میتونیم مانند بردار 'OO، طول تصویر بردار O'M را بر روی محور x ها را هم حساب کنیم. این طول برابر میشود با:
بنابراین تصویر نقطه ی M روی محور x ها برابر میشه با:
با استدلالی مشابه، تصویر نقطه ی M روی محور y ها هم برابر میشه با:
اما این جوابها به خودی خود ارزش ندارند. چرا که باید در هر لحظه محاسبه کنیم که
اما خودمان برای راحتی، قرارداد کردیم که
با این حساب و در نهایت مختصات نقطه ی مرجع متحرک در هر لحظه ی دلخواه t برابر است با:
******************
پنجشنبه
7 / 2 / 91



دیدگاه