سلام ...................
در این تاپیک قرار هست در مورد تکنیکی در پردازش تصویر به نام Morphological Image Processing صحبت کنیم .. مطالبی که در این تاپیک مطرح میشه، موارد و کاربردهایی از این تکنیک در پردازش تصویر هست که به تازگی مورد استقبال پروسه های پردازشی قرار گرفتن .. هدف اصلی این تاپیک آشنایی با این تکنیک و کاربردهای اون به عنوان یک ابزار قدرتمند در پردازش تصویرهست و بیشتر سعی بر این بوده که مطالب به صورت مفهومی به همراه مثال مطرح بشن تا درک موضوعات ساده تر و مفهومی تر باشه و از مطرح کردن روابط ریاضی صرف در اون، تا حد ممکن اجتناب شده ..
در ابتدا باید با واژه ی Morphology آشنا بشیم و ببینیم چه ویژگی هایی برای اون پیش بینی شده .. از نظر لغوی این کلمه به معنای ریخت یا ظاهر هست و صفت اون (Morphological) به معنای ریخت شناسی یا ظاهر شناسی است .. اما منظورمون از ریخت دقیقا چیه؟ از نظر فیزیکی ، در حقیقت تمام نیازی که ما از این شاخه طلب میکنیم این هست که بتونه در تحلیل ، آنالیز و استخراج ویژگی های فرمیک تصویر به ما کمک کنه و در نهایت مارو قادر کنه تا بتونیم بر روی Shape تصویرمون قضاوت داشته باشیم .. یعنی پس از استفاده از این تکنیک؛ ما قادر خواهیم بود نسبت به Shape تصویرمون ادراک داشته باشیم (با محدودیت هایی که برای Region ها در نظر میگیریم ..) .. تصاویر زیر رو ملاحظه کنید .. تصویر سمت چپ، image ما هست و تصویر سمت راست Shape اون ..


همونطور که احتمالا متوجه شدید، منظور از Shape یک شمای کلی از Structure تصویر هست که بازگو کننده ی فرم کلی اون خواهد بود .. از این فرم نمیتونیم Feature (ویژگی ساختاری تصویر ..) ارزشمندی استخراج کنیم، اما ارزش های دیگه ی اون باعث شده که ما از Shape در خیلی موارد به عنوان تنها راه حل ممکن، استفاده کنیم ..
از نظر ریاضی، استفاده ای که از این تکنیک میکنیم؛ اینه که بتونیم تصویرمون رو با مجموعه های ریاضی معادل کنیم .. در حقیقت هر مجموعه بازگوکننده ی یک آبجکت در تصویر هست به این معنا که اگه آبجکتی در تصویر وجود داشته باشه که تمام پیکسل هاش سیاه باشه، میتونه باز گو کننده ی یک مجموعه ی مستقل در فضای Morphology باشه .. برای تصاویر باینری (فضای رنگی باسنری ..) معادل ریاضی که برای مجموعه ها در نظر گرفته میشه، مجموعه های دوبعدیه، به این معنا که اعضای اون عضو مجموعه ی Z^2 هستن .. بنابر این اگه آبجکت سیاه در تصویر ما موجود باشه، اعضای مجموعه مختصات مولفه های سیاه درون آبجکت هستن ؛ لذا تونستیم از آبجکت یه تعریف ریاضی ارائه کنیم .. اگه فضای رنگی ما Gray Level باشه ، بعد مجموعه ی ما به فضای Z^3 میره و اینجا مجموعه ی ما میشه سه بعدی که دو بعدش اختصاص دارن به مختصات پیکسل ها و یه بعدش هم اختصاص پیدا میکنه به مولفه های رنگی (Color Distribution Factor) آبجکت مورد نظردرون تصویر .. همون طور که متوجه شدید ، با بالا بردن ابعاد مجموعه در فضای Z میتونیم انعطاف فضاهای رنگی دیگه ای رو هم برای آبجکت ها در نظر بگیریم ..
در نتیجه برای آشنایی با این شاخه باید با مجموعه ها و روابط اونها آشنا بشیم .. روابطی که از همه بیشتر در این مبحث کاربرد دارن رو خیلی مختصر بیان میکنیم ..
-- Union یا اجتماع .. حکم OR در منطق دیجیتال ..
-- Intersection یا اشتراک .. حکم AND در منطق دیجیتال ..
با توجه به مجموعه های در نظر گرفته شده ی A و B میتونید روابطی که بر مبنای دو رابطه ی بالا تعریف میشه، ببینید ..

-- Translation یا تغییر مکان مختصاتی ( یه تبدیل جمع برای i و j .. ) .. برای بیان این خاصیت بهتره که در ابتدا به رابطه ی ریاضی اون بپردازیم و در انتها هم تحلیل گرافیکی اون رو نشون بدیم ..

همون طور که مشاهده میکنید، اساس این خاصیت بر میگرده به جمع یک مختصات آفست با مختصات پیکسل های تصویر اولیه ی شما (مجموعه ی شما ..) .. در حقیقت (a,b) اعضای مجموعه ی شما هستن (نقاط آبجکتتون ..) که با مقدار ثابت (x,y) جمع شدن و تصویر حاصل ، به اندازه ی (x,y) از Initial Origin فاصله گرفته .. در شکل زیر میتونید نتیجه ی گرافیکی اون رو ببینید ..

-- Reflection نگاشت تقارن .. این تبدیل هم عمل تقارن رو روی مجموعه ی ما پیاده سازی میکنه، تقارن نسبت به محور x و y .. برای مشخص شدن این خاصیت، رابطه ی ریاضی اون رو بررسی میکنیم ..

همونطور که در رابطه ی بالا هم مشاهده میکنید، این خاصیت ، روی اعضای مجموعه تبدیلی رو انجام میده که اعضا معادل های قرینه ی خودشون رو در صفحه ی مختصات (کارتزین ..) میبینن .. یعنی x به –x نگاشت میشه و y به –y .. نتیجه ی گرافیکی اون رو هم میتونید در شکل زیر ببینید ..

و ...

همون طور که در شکل های بالا هم ملاحظه میکنید، تقارن نسبت به محورها کاملا مشهود هست ..
تا اینجا با اساسی ترین روابط و خواص مجموعه ها آشنا شدیم .. در پست بعد به بررسی دو تعریف مهم و اساسی در این شاخه می پردازیم .. با تشکر از همراهی دوستان .. موفق باشید ..







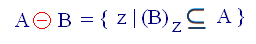



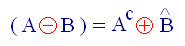




























دیدگاه